具有动态调节特性的光伏制氢双阵列直接耦合系统优化策略
0 引言
第75届联合国大会上,中国提出2个阶段碳减排奋斗目标:二氧化碳排放力争于2030年前达到峰值,2060年前实现碳中和。为高质量实现该目标,就必须走绿色低碳的道路[1]。氢能是一种热值高,方便储存和转运的二次能源,可以充当能源缓存载体提高系统韧性,降低工业产生的碳排放[2-3],在“双碳”路径中发挥至关重要的作用。利用可再生能源制氢,是清洁、高效制取“绿氢”的未来发展趋势,具有重大战略意义[4-6]。可再生能源包括太阳能、风能、水能等,其中,光伏制氢是利用光伏面板和商业上可获得的电解水装置来生产氢气,是国内外专家和学者研究的热点问题之一[7]。
在光伏制氢(photovoltaic electrolysis,PVE)系统中,光伏发电为直流电,与电解水装置的连接方式分为直接耦合和间接耦合。间接耦合是光伏板通过控制器、DC/DC变换器为电解槽供电,是绝大部分系统所采用的连接方式[8]。但变换器的选择需要考虑众多因素,例如升压转换比、电磁干扰、输出电流纹波等。此外高效率的变换器需要更多的元器件,无法同时满足系统成本和能量损失要求,仍有一段长期的攻关过程[9],于是直接耦合的研究变得尤为关键。通过直接将光伏板与电解槽相连,结构相对简单,能量损失较低,能实现光伏充分消纳,但取而代之的是光伏板需要与电解水装置的电压、电流相匹配[10],对此国内外学者进行了多方面的研究。文献[11]分析PVE直接耦合系统的最佳运行条件,通过帝国主义竞争算法(imperialist competitive algorithm,ICA)同时考虑电解槽制氢量最大化和光伏能量传递损失最小化2个目标来优化系统。文献[12]使用双重遗传算法(genetic algorithm,GA)优化直接耦合系统工作温度,保持接近光伏阵列最大功率点的运行条件,最小化过剩发电量。文献[13]加入DC/DC变换器对直接耦合系统进行改进,设计了一种耦合算法来调控最佳占空比,使光伏阵列最大功率发电的同时电解槽能工作于安全区域。以上,算法仅针对当前系统状态下的最优解问题,并不能从本质的电气特性角度对系统进行改善;而利用变换器来调控,本身就脱离了间接耦合,会产生额外的能量损失,也不能被广泛推广,应考虑从实际电压与电流的匹配角度来分析。文献[14]使用GaP/GaAS/Ge型光伏电池与电解槽直接耦合,通过使工作点尽可能接近最大功率点以提高整体效率。文献[15]理论分析了光伏阵列和电解槽的实验特性,实现电解槽和光伏阵列伏安特性最相匹配。文献[16]采用光伏电流法(photovoltaic current method),根据光伏输出电流变化,动态调节电解槽内部组成结构,时刻保持较高的能量传递效率。
当前,对直接耦合制氢系统的研究主要集中在其结构设计上,调节策略分析得较少,导致系统无法适应太阳能的随机性和波动性,动态调节性差,光伏消纳不稳定。针对以上问题,文献[16]采用光伏电流法对系统的动态性能进行了改进,但只考虑了电解槽内部单元的串联组合形式,并没有充分挖掘出电解槽本身工作特性,调节参数单一化导致系统仍存在一定能量损耗,对电解槽的产氢速率也考虑不足,不能达到最优效益。
鉴于现有研究工作的不足,本文提出光伏阵列–质子交换膜(proton exchange membrane,PEM)电解槽阵列的双阵列直接耦合系统模型。PEM选用具有良好气体分离性和离子传输性的全氟磺酸(Nafion)材料,能有效阻止电子传递,提高系统安全性。同时PEM电解技术拥有较好的动态特性,通常处于ms级,能与太阳能的波动性进行匹配,适合光伏制氢系统的研究。随后详细分析了PEM电解槽阵列的工作特性,并在梳理电解槽阵列特性及工作约束的基础上,提出了一种动态调节优化策略,最后仿真验证了所提策略的有效性。本研究对光伏制氢直接耦合系统的运行可提供一定参考价值。
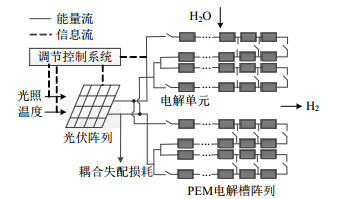
1 光伏制氢双阵列直接耦合系统 1.1 系统整体结构本文所研究的PVE双阵列直接耦合系统整体结构如图 1所示,主要由光伏阵列和PEM电解槽阵列构成,光伏阵列和电解槽阵列分别是由若干个光伏组件、电解单元串并联组成。其中光照强度和环境温度是影响光伏阵列输出功率的关键因素,光伏阵列将太阳能转化为电能,输送给电解水装置制取氢气。直接耦合对两者电压、电流的匹配要求较高,通常存在一定程度的耦合失配问题,产生少量能量损耗。
|
图 1 光伏制氢双阵列直接耦合系统结构 Fig. 1 Structure of dual array direct coupling system for photovoltaic hydrogen production |
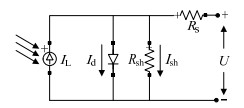
光伏电池利用半导体的光生伏特效应将光能直接转为电能,其等效模型一般采用带有串并联电阻的单二极管等效电路,如图 2所示。
|
图 2 光伏电池等效电路 Fig. 2 Equivalent circuit of photovoltaic cell |
根据图 2电路分析,光伏电池的一般方程为
| $ I={I_{ ext{L}}} - {I_{ ext{d}}}\left\{ {\exp [\frac{{q(U + {R_{ ext{s}}}I)}}{{nK{T_{{ ext{pv}}}}}}] - 1} \right\} - \frac{{U + {R_{ ext{s}}}I}}{{{R_{{ ext{sh}}}}}} $ | (1) |
式中:I为光伏输出电流;U为光伏输出电压;IL为光生电流;Id为二极管反向饱和电流;Rsh为分流电阻;Ish为经过该电阻的电流;Rs为寄生电阻;q为单位电荷;K为波尔兹曼常数;n为二极管品质因子;Tpv为光伏电池工作温度。
该模型参数较多,不适合进行定量分析。一般来说,Rs的值很小(接近于0),Rsh趋近于无穷大,可忽略寄生电阻和流过分流电阻的电流。当二极管正向导通时电阻相比Rs值大得多,流入二极管的电流较小,此时可令IL=Isc,C1Isc=I0,C2Uoc=nKTpv/q,其简化的工程模型为式(2)。考虑光伏的最大功率输出,同时式(2)中指数项远大于1,可忽略“?1”项,C1、C2表达为式(3)。
| $ I={I_{{ ext{sc}}}}\{ 1 - {C_1}[\exp (\frac{U}{{{C_2}{U_{{ ext{oc}}}}}}) - 1]\} $ | (2) |
| $ \left\{ {\begin{array}{*{20}{l}} {{C_1}=(1 - \frac{{{I_{{ ext{mp}}}}}}{{{I_{{ ext{sc}}}}}})\exp (\frac{{ - {U_{{ ext{mp}}}}}}{{{C_2}{U_{{ ext{oc}}}}}})} \\ {{C_2}=(\frac{{{U_{{ ext{mp}}}}}}{{{U_{{ ext{oc}}}}}} - 1){{[\ln (1 - \frac{{{I_{{ ext{mp}}}}}}{{{I_{{ ext{sc}}}}}})]}^{ - 1}}} \end{array}} \right. $ | (3) |
式中Isc、Uoc、Imp、Ump分别为电池的短路电流、开路电压、最大功率点处的电流与电压,这些参数可以直接从产商得到。则由多个光伏电池或组件构成的光伏阵列模型可表示为
| $ I={N_{ ext{p}}}{I_{{ ext{sc}}}}\{ 1 - {C_1}[\exp (\frac{U}{{{C_2}{N_{ ext{s}}}{U_{{ ext{oc}}}}}}) - 1]\} $ | (4) |
式中Np和Ns分别为光伏阵列中组件并联数和串联数。光伏阵列通常以最大功率输出,其最大功率点(maximum power point,MPP)的推导过程见附录A。
1.2.2 PEM电解槽阵列模型质子交换膜电解水装置的宽范围运行电流密度、快速启停、灵活功率调节等特性,更适用于匹配可再生能源的波动性和间歇性,有望成为电网调峰的理想能量存储转换装置[17]。同时,由于管道输氢需要加压氢气,具有较高压强的PEM电解槽拥有与储氢需求匹配的天然优势[18],故本文选用PEM电解槽进行研究。
电解总电压Uel由可逆电压、欧姆过电势、活化过电势、扩散过电势组成。
| $ {U_{{ ext{el}}}}={U_{{ ext{rev}}}} + {U_{{ ext{ohm}}}} + {U_{{ ext{act}}}} + {U_{{ ext{diff}}}} $ | (5) |
式中:Urev为可逆电压;Uohm为电阻产生的欧姆过电势;Uact为电化学反应产生的过电势;Udiff为传质扩散引起的扩散过电势,占比较小,通常可以忽略。
可逆电压通过能斯特(Nerst)方程求得,即
| $ \begin{gathered} {U_{{ ext{rev}}}}=1.229 - 0.009({T_{{ ext{el}}}} - 298.15) + \hfill \\ \;\;\;\;\;\;\;\;\;\frac{{R{T_{{ ext{el}}}}}}{{2F}} imes \ln (\frac{{{P_{{{ ext{H}}_2}}}P_{{{ ext{O}}_2}}^{0.5}}}{{{\alpha _{{{ ext{H}}_{ ext{2}}}{ ext{O}}}}}}) \hfill \\ \end{gathered} $ | (6) |
式中:
欧姆过电势可表示为
| $ {U_{{ ext{ohm}}}}=\frac{\delta }{\sigma }i $ | (7) |
式中:δ为膜电极厚度;i为电流密度;σ为膜的传导率,与膜的水含量和工作温度有关,见式(8)。
| $ \sigma=(0.005139\lambda - 0.00326)\exp [1268(\frac{1}{{303}} - \frac{1}{{{T_{{ ext{el}}}}}})] $ | (8) |
式中λ为膜中磺酸根基团所含水分子数,在膜全湿的情况下,λ取14。
活化过电势分为阳极和阴极极化过电势Uact, an、Uact, ca,计算公式为
| $ \left\{ {\begin{array}{*{20}{c}} {{U_{{ ext{act, an}}}}=\frac{{R{T_{{ ext{el}}}}}}{F}{{\sinh }^{ - 1}}(\frac{i}{{2{i_{{ ext{an}}}}}})} \\ {{U_{{ ext{act, ca}}}}=\frac{{R{T_{{ ext{el}}}}}}{F}{{\sinh }^{ - 1}}(\frac{i}{{2{i_{{ ext{ca}}}}}})} \end{array}} \right. $ | (9) |
式中ian、ica分别为阳极和阴极交换电流密度,与电极材料、工作温度等有关。
电解槽阵列内部的单元排列与光伏阵列类似,若组成的电解单元参数一致,其数学模型为
| $ \left\{ {\begin{array}{*{20}{l}} {{U_{{ ext{stack}}}}={n_{ ext{s}}}{U_{{ ext{el}}}}} \\ {{I_{{ ext{stack}}}}={n_{ ext{p}}}{I_{{ ext{el}}}}} \end{array}} \right. $ | (10) |
式中:np和ns分别为电解槽阵列单元并联数和串联数;Iel为流过电解槽单元电流。PEM电解槽阵列产氢速率表达式见附录A,可以发现:单位时间内的产氢量与电流大小和串联单元个数成正比。
2 PEM电解槽阵列工作特性PEM电解槽阵列拥有与光伏阵列类似的复杂结构,相比简单的串联组合能充分表现出自身的工作特性,避免对电解槽分析不全面而产生不必要的能量损耗。
光伏阵列与电解槽阵列的I-U曲线表达式见式(4)(10)。对于理想的直接耦合系统,双方的电压、电流应相匹配,故两曲线的交点即为系统的工作点。常规方法是使该工作点尽可能接近MPP,方法过于简单,且没有考虑氢气注入系统的安全稳定运行。需要指出的是,由于电解槽内部材料的特性,运行功率不能过低,否则会造成氢、氧互串发生超过爆炸极限的风险[19],所以需要对电解槽I-U曲线进行区间限制。本文直接考虑电解槽阵列I-U曲线的线性稳定部分,此时工作曲线的表达式见式(11),a, b分别对应线性方程的一次项和常数项系数。用能量传递效率ηc来衡量工作点与MPP的接近程度,表达式为式(12),其中,P为工作点处功率,Pm为光伏最大输出功率。
| $ {I_{{ ext{el}}}}=a\frac{{{n_{ ext{p}}}}}{{{n_{ ext{s}}}}}{U_{{ ext{el}}}} + b{n_{ ext{p}}} $ | (11) |
| $ {\eta _{ ext{c}}}=P/{P_{ ext{m}}} $ | (12) |
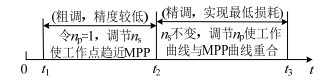
PEM电解槽阵列工作特性可以从式(11)分析得出,该曲线是一条经过点(?bns/a,0)、斜率为np/ns的直线,串联单元个数与曲线的横向移动直接相关,并联单元个数对工作曲线的斜率起决定性控制作用。临界工况下,当np=1时,系统等效于仅考虑串联组合的情况,可以发现,斜率始终保持较低数值,ns对斜率的控制范围较小,导致曲线走势较平缓,无法紧凑追踪MPP变化。而对于电解槽阵列结构,随着调节参数个数的增加,设置适合的np和ns可使得电解槽阵列的工作曲线更接近于最大功率曲线,两者的动作时序关系如图 3所示,先调ns进行粗调,后调np提高整体追踪精度。
|
图 3 串并联单元调节动作时序 Fig. 3 Regulating action sequence of series parallel unit |
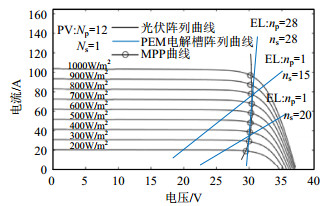
ns和np通过继电器开关进行调控,继电特性能使开关迅速接受电信号,实时性较好(ms级)[20]。不同组成结构的电解槽阵列与光伏阵列在光照变化下的工作轨迹如图 4所示。观察发现:仅考虑单元串联组合的电解槽(np=1)工作曲线斜率平缓,只在小范围光照区间内,工作点才能高效率跟踪MPP,在其他情况下系统的能量传递效率均不理想。采用光伏电流法对串联单元个数进行动态调节,虽说对传递效率有一定改善,但由于调节参数的局限性,在某些光照下,也很难找到能量传递效率较高的组合形式,这大大增加了系统动态调节的操作难度。而电解槽(electrolyzer,EL)阵列相比却能表现出优异的MPP跟踪能力,工作曲线与最大功率曲线大面积重合,充分利用到电解槽的工作特性。
|
图 4 光伏阵列与PEM电解槽阵列工作轨迹 Fig. 4 Working track of photovoltaic array and PEM electrolyzer array |
上文从曲线表达式角度阐述了PEM电解槽阵列的工作特性,限制电解槽的工作点位于曲线的线性区域,此时系统预期目标已从工作点接近MPP转变为工作曲线与MPP曲线的重合。
由于MPP曲线的自变量次数相比电解槽工作曲线较高,针对一次函数与高次函数的重合问题,依据求根判据可得两曲线最多存在2个交点。即在固定参数下,仅能保证电解槽在2个准确光照强度下才能跟踪MPP,其他情况由于高次函数的凹凸特性,能量效率会大幅度降低。这就导致电解槽需要频繁变动串并联结构才能跟踪,降低了系统的使用寿命。为了方便研究曲线重合问题,对MPP曲线进行降次处理,通过线性拟合转变为式(13)的形式,其中A、B为对应方程的相关参数。
| $ {I_{{ ext{pv}}}}=A\frac{{{N_{ ext{p}}}}}{{{N_{ ext{s}}}}}{U_{{ ext{pv}}}} + B{N_{ ext{p}}} $ | (13) |
并基于最小二乘法对待定参数(a, b, A, B)进行精确估计,记含有n个自变量T(t1, t2, ···, tn)和p维待定参数向量θ=(θ1, θ2, ···, θp)Τ的模型为
| $ \mathit{\boldsymbol{y}}=\mathit{\boldsymbol{f}}(\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{ heta }}) + \mathit{\boldsymbol{\varepsilon }} $ | (14) |
式中:y为输出;f为一般函数向量;ε为n维随机误差向量,服从二项分布。参数递推公式的矩阵表达为式(15)(16),k为递推次数。
| $ {\mathit{\boldsymbol{ heta }}_{k + 1}}={\mathit{\boldsymbol{ heta }}_k} + {[{\mathit{\boldsymbol{J}}^{ ext{T}}}({\mathit{\boldsymbol{ heta }}_k})\mathit{\boldsymbol{J}}({\mathit{\boldsymbol{ heta }}_k})]^{ - 1}}{\mathit{\boldsymbol{J}}^{ ext{T}}}({\mathit{\boldsymbol{ heta }}_k})[\mathit{\boldsymbol{y}} - \mathit{\boldsymbol{f}}(\mathit{\boldsymbol{T}}, {\mathit{\boldsymbol{ heta }}_k})] $ | (15) |
| $ \mathit{\boldsymbol{J}}({\mathit{\boldsymbol{ heta }}_k})={\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {f_1}(\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{ heta }})}}{{\partial { heta _1}}}}& \ldots &{\frac{{\partial {f_1}(\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{ heta }})}}{{\partial { heta _p}}}} \\ \vdots & \ddots & \vdots \\ {\frac{{\partial {f_n}(\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{ heta }})}}{{\partial { heta _1}}}}& \cdots &{\frac{{\partial {f_n}(\mathit{\boldsymbol{T}}, \mathit{\boldsymbol{ heta }})}}{{\partial { heta _p}}}} \end{array}} \right]_{\mathit{\boldsymbol{ heta }}={\mathit{\boldsymbol{ heta }}_k}}} $ | (16) |
最小二乘法可使拟合结果接近无偏估计,给出的相关系数更能反映拟合的显著性水平[21]。通过算法得出a=79.44,b=?83.67,A=4.30,B=?124.6,其相关系数分别为
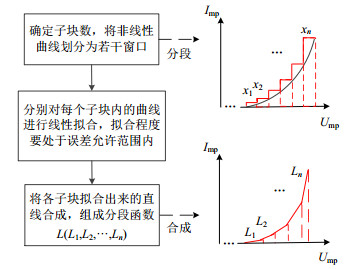
电解槽阵列的结构确定是动态调整的前提,为计算最适合当前光强下的电解槽结构,需先进行适当的线性拟合,然而光伏组件最大功率曲线的非线性使得确定电解槽阵列的最优结构较为困难。本节提出一种曲线分段线性再合成的方法,依据最小二乘法“残差平方和最小”的基本准则,采用不等分法将输出曲线拆分为若干子块x1、x2···xn。子块个数从初始值逐渐迭代,分别对每个子块内的曲线线性化处理,根据相关系数确定分段位置以便达到最优化,直到各子块内曲线拟合精度满足要求,则停止迭代,子块划分结束。最后通过分段部分重叠的方式进行合成,消除各子块边界处存在的跳变问题,步骤如图 5所示。
|
图 5 光伏最大功率曲线分段线性化具体步骤 Fig. 5 Piecewise linearization of photovoltaic maximum power curve |
基于PEM电解槽阵列工作特性和光伏最大功率曲线的非线性制定多子块动态调节优化策略,旨在根据子块的分划情况,对电解槽I-U曲线的线性稳定部分进行匹配设计。令Upv=Uel,Ipv=Iel,确定不同光照强度下电解槽阵列对应的结构,动态调节阵列参数。子块的划分存在一定约束条件,假设MPP曲线被分为i个子块(i=1, 2, ···, n)。
1)拟合相关性约束。
| $ \left\{ {\begin{array}{*{20}{l}} {R_{ ext{b}}^2 \leqslant R_i^2 \leqslant 1} \\ {0 \leqslant \sum {r_i^2 \leqslant \sum {r_{\max }^2} } } \\ {0 \leqslant S_i^2 \leqslant S_{\max }^2} \end{array}} \right. $ | (17) |
式中:Ri、
2)取整偏差约束。
确定各子块拟合直线Li后,还需确保电解槽工作曲线能找到合适的np和ns与Li尽可能重合,对求出的串并联个数理论值与实际值之间的差值Δnp, i、Δns, i进行约束。
| $ \left\{ {\begin{array}{*{20}{c}} {\Delta {n_{{ ext{p, }}i}}={ ext{|}}{n_{{ ext{p, }}i}} - n_{{ ext{p, }}i}^ * { ext{|}} \leqslant 0.05} \\ {\Delta {n_{{ ext{s, }}i}}={ ext{|}}{n_{{ ext{s, }}i}} - n_{{ ext{s, }}i}^ * { ext{|}} \leqslant 0.05} \end{array}} \right. $ | (18) |
式中:
综上所述,双阵列系统的动态调节优化策略见图 6。

|
图 6 双阵列系统动态调节优化策略流程 Fig. 6 Dynamic adjustment optimization strategy flow of dual array system |
基于MATLAB/Simulink仿真软件,根据图 1搭建系统模型,验证本文所提动态调节优化策略的有效性。选用1STH-245-WH型光伏组件为参考对象,在标准条件下各单元的主要参数见附录A表 A1、A2,此时光伏阵列额定功率为3kW。
为阐述本文所提双阵列系统下的动态调节优化策略与常规方法及文献[15]所提策略的区别,利用以下3个系统对各策略进行对比分析:
1)假设系统1。常规匹配方法。电解槽内部单元个数确定后,在整个工作周期内保持不变。
2)假设系统2。光伏电流法。引入动态调节参与系统运行,仅考虑单元串联组成的电解槽模型。
3)假设系统3。动态调节优化策略,在系统2研究基础上,考虑电解槽阵列的复杂串并联模型。
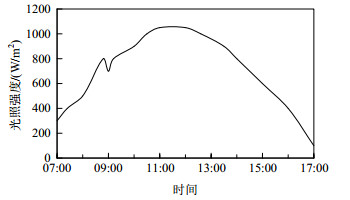
4.1 有效性分析为了体现出动态调节优化策略的有效性,在简单场景下分析各系统的能量传递情况,其中光照强度变化如图 7所示。
|
图 7 常见场景下的光照变化情况 Fig. 7 Illumination changes in common scenes |
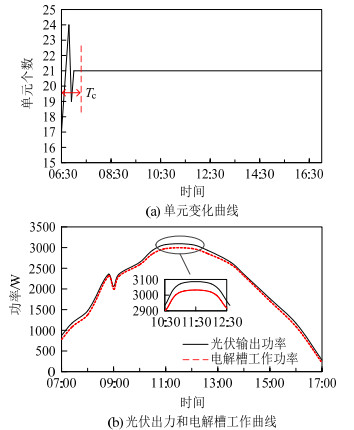
该场景下,系统1内部单元个数变化和功率消纳情况如图 8所示,其中Tc为寻找与光伏阵列匹配电解槽的试验时间。常规方法需要将光伏与不同结构的电解槽进行匹配尝试,观察效果后从中选出最适合的串联结构,存在一定时间消耗,整体过程较缓慢,且试验完后电解槽结构不会发生改变。从图 8可以看出:21个电解槽单元串联组成的电解槽结构与光伏匹配最优;光伏输出功率与光照强度直接相关,不同光强下的能量传递效率有明显差异,ηc对光照较为敏感;电解槽不能充分吸收光伏最大输出功率,能量损失较大,11:30时差值甚至达到了55W,系统1跟踪MPP性能较弱。
|
图 8 单元变化、光伏出力、电解槽工作曲线 Fig. 8 Curves of unit change, photovoltaic output and electrolyzer input |
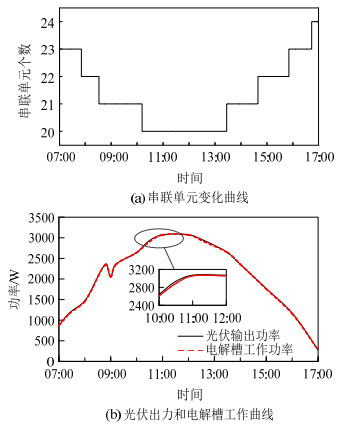
系统2是在系统1的基础上提出的,通过观察光伏输出电流变化,动态调节串联单元来改善电解槽跟踪MPP的能力,以解决常规策略中能量传递效率对光照敏感问题,其仿真结果如图 9所示。串联单元个数在工作周期内根据电流动态调整,正午时段,电解槽主要以20个单元串联组成形式工作。在消纳光伏功率方面,与系统1相比有所提高,表明动态调节策略的引入能有效改善系统,对该方向的研究还是很有必要的。但该策略在某些时间段还存在较多损耗,10:30左右光伏输出功率为2935W,电解槽实际吸收功率仅2904W,能量损失达到1.06%,仍需进行改进。
|
图 9 串联单元变化、光伏出力及电解槽工作曲线 Fig. 9 Curves of series unit change, photovoltaic output and electrolyzer input |
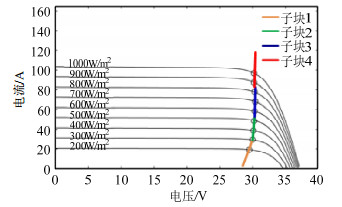
系统3以电解槽阵列为主体进行分析。首先对光伏最大功率曲线进行分段线性化处理,根据相关系数和约束条件确定子块的拆分个数及分段位置。最终曲线被分为4个子块,划分情况见附录A表 A3,对各子块分别拟合再合成,得到MPP曲线分段线性化结果,见图 10。
|
图 10 MPP分段线性化结果 Fig. 10 Piecewise linearization of MPP curve |
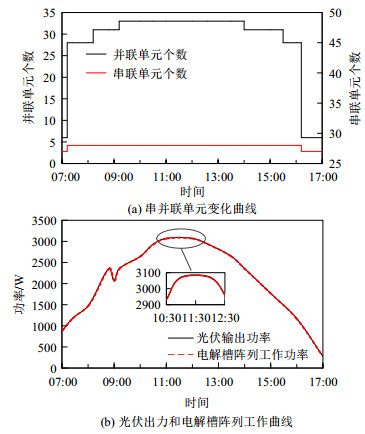
采用动态调节优化策略对分段线性后的MPP曲线进行分析,结果见图 11。可以看出:电解槽阵列根据光强变化迅速调整内部的串并联单元结构。整体上,串联单元的调节次数较少,只在低光强到中光强的跨度上起作用,主要通过并联单元进行精确调节,灵活性更好,与系统2相比表现出较高的MPP跟踪性能。10:30—12:30时,能量传递效率保持在99.5%以上。甚至在正午时段,光伏输出3072W电能,而电解槽阵列的吸收功率高达3068W,能量损失仅0.01%,几乎无损耗。该策略实现了制氢系统在波动工况下对光伏能量的充分消纳。
|
图 11 串并联单元变化、光伏出力及电解槽阵列工作曲线 Fig. 11 Curve of series parallel unit change, photovoltaic output and electrolyzer array input |
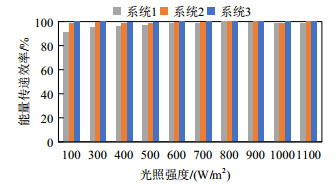
不同光照下各系统的能量传递效率如图 12所示。其中系统1整体的能量传递效率较低,当光强为100W/m2时,效率仅为91.2%,且对外界光强变化十分敏感;相比之下,系统3在各光强下表现出优秀的能量传递效率,均在99.5%以上,损失较小,验证了动态调节优化策略的可行性;系统2因为没有充分利用到电解槽工作特性,当光强为1000W/m2时,效率为98.8%,仍有一定能量损耗,而且由于调节参数过于单一,动态调节特性也有差异,4.2节将具体介绍。
|
图 12 各系统在不同光照下的能量传递效率 Fig. 12 Energy transfer efficiency of each system under different illumination |
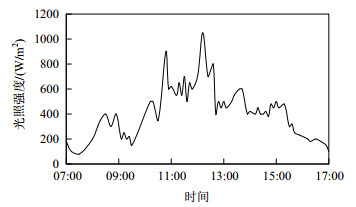
在复杂场景(某阴雨天)下分别对系统2、3的动态调节特性进行分析,光照变化如图 13所示。
|
图 13 阴雨天下的光照变化情况 Fig. 13 Illumination changes in rainy days |
两系统内部单元变化情况如图 14所示。观察发现:光照强度随机变化时,光伏输出电流也同步改变,变化轨迹与光照类似。系统2根据输出电流的变化对系统内部单元进行调节,电流上升时减少单元个数,反之则增加单元个数。而系统3直接根据工作曲线与MPP曲线的对应关系作出调整,将光照强度进行不同区域的划分,各个区域对应电解槽阵列的不同结构。从图 14看出,串联单元个数变化时,并联单元也变化,可见该策略下系统只存在2种调节工况:1)仅调节并联单元个数。2)同时调节串联和并联单元个数。并联单元的变化情况直接限制系统3的结构变化。
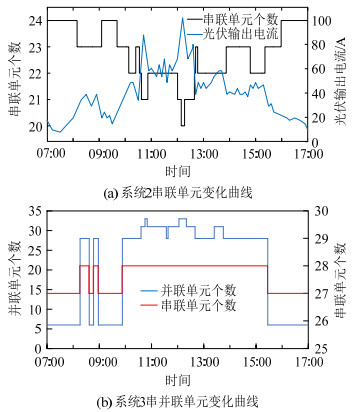
|
图 14 系统2、3内部单元变化情况 Fig. 14 Changes of internal units in system 2 and 3 |
表 1对两系统内部单元的变化进行了比较,左右两边数据分别代表串联单元、并联单元的相关数据。可以发现:系统2整体变化较频繁,最快时仅运行4.43min就变换了电解槽结构;而系统3把最低利用时长提高到了5min,最高利用时长从68min提高到了102min。在整个工作周期内,系统3相比于系统2变更次数减少了2次,可见,本文所提策略的动态调节特性较为适用。
|
|
表 1 系统2、3单元变化对比情况 Table 1 Comparison of changes in system 2 and 3 units |
各系统在不同光照强度下的产氢速率如图 15所示。系统1、2的产氢速率相差不大,表明光伏电流法仅改善了系统的能量传递效率,并没有考虑到制氢系统的产氢量。而系统3相比其他2个系统,产氢速率大大增加,并且系统间的速率差异随光强增大逐渐上升,最终趋于稳定。当光照强度为1000W/m2时,系统3产氢速率比系统1、2高出28%,充分体现出该调节策略的优越性。

|
图 15 各系统在不同光照下的产氢速率情况 Fig. 15 Hydrogen production rate of each system under different illumination conditions |
本文建立光伏制氢直接耦合系统精确模型,针对现有研究在波动工况下灵活性差等问题,基于双阵列结构,提出一种动态调节优化策略,实现了光伏最优消纳。理论和仿真证明了以下结论:
1)构建光伏阵列—PEM电解槽阵列的双阵列复杂模型,充分挖掘出电解槽本身工作特性,将直接耦合制氢系统的匹配指标从原本的工作点接近MPP转变为工作曲线与最大功率曲线的重合问题。
2)对光伏最大功率曲线分段线性化进行降次处理,可以有效解决高次曲线凹凸性造成的影响,防止电解槽结构的频繁变动,提高系统使用寿命。
3)采用动态调节优化策略显著提高了系统整体的能量传递效率,高光强时传递效率达到99.9%,其他情况也能维持在99.5%以上,几乎实现无损耗运行;其次优化了制氢系统的产氢能力,产氢速率相比提升了28%;动态特性上,将各单元最低利用时长提高到5min,最高利用时长提高到了102min,同时调节参数的增加也改善了系统灵活性。
本文对于PEM电解槽阵列的研究仅局限于内部单元结构统一的情况,可进一步对由不同参数单元组合而成的电解槽阵列进行具体探讨。
附录见本刊网络版(http://www.dwjs.com.cn/CN/1000-3673/current.shtml)。
附录A1)光伏最大功率点推导
光伏阵列的输出功率可表示为
| $ P=UI={N_{ ext{p}}}{I_{{ ext{ph}}}}U - {N_{ ext{p}}}{I_{ ext{0}}}U[\exp (\frac{{qU}}{{{N_{ ext{s}}}nK{T_{{ ext{pv}}}}}}) - 1] $ | (A1) |
令dP/dV=0,并与公式(4)联立,可得到最大功率点处的电压Ump和电流Imp,获得该场景下的MPP曲线。
| $ \begin{gathered} \frac{{{ ext{d}}P}}{{{ ext{d}}U}}={N_{ ext{p}}}{I_{{ ext{ph}}}} + {N_{ ext{p}}}U\frac{{{ ext{d}}{I_{{ ext{ph}}}}}}{{{ ext{d}}U}} + {N_{ ext{p}}}{I_0} - {N_{ ext{p}}}{I_0} imes \hfill \\ \begin{array}{*{20}{c}} {}&{\;\;\;\;[\exp (\frac{{qU}}{{{N_{ ext{s}}}nK{T_{{ ext{pv}}}}}})\frac{q}{{{N_{ ext{s}}}nK{T_{{ ext{pv}}}}}} + \exp (\frac{{qU}}{{{N_{ ext{s}}}nK{T_{{ ext{pv}}}}}})]} \end{array} \hfill \\ \end{gathered} $ | (A2) |
| $ \frac{{{I_{{ ext{ph}}}} + {I_0}}}{{{I_0}}}=[(\frac{{q{U_{{ ext{mp}}}}}}{{{N_{ ext{s}}}nK{T_{{ ext{pv}}}}}}) + 1]\exp (\frac{q}{{nK{T_{{ ext{pv}}}}}}\frac{{{U_{{ ext{mp}}}}}}{{{N_{ ext{s}}}}}) $ | (A3) |
2)PEM电解槽阵列产氢速率推导
根据电化学原理,PEM电解槽单元的实际产氢速率如式(A4)所示:
| $ \left\{ {\begin{array}{*{20}{l}} {{q_{{ ext{H2}}}}={\eta _{ ext{F}}}\frac{{{ ext{3600}}{V_{{ ext{H2}}}}{I_{{ ext{el}}}}}}{{2F}}} \\ {{\eta _{ ext{F}}}=\frac{{{{({I_{{ ext{el}}}}{ ext{/}}A)}^2}}}{{{f_1} + {{({I_{{ ext{el}}}}{ ext{/}}A)}^2}}}{f_2}} \end{array}} \right. $ | (A4) |
式中:qH2为产氢速率(m3/h);VH2为氢气的摩尔体积;A为电解槽的活性面积;ηF称为法拉第效率;f1、f2为法拉第效率相关参数。
对于由np×ns单元组成的电解槽阵列,其产氢速率为
| $ {q_{{ ext{H2}}}}={\eta _{ ext{F}}}\frac{{3600{V_{{ ext{H2}}}}{n_{ ext{s}}}{n_{ ext{p}}}({I_{{ ext{el}}}}{ ext{/}}{n_{ ext{p}}})}}{{2F}}={\eta _{ ext{F}}}\frac{{3600{V_{{ ext{H2}}}}{n_{ ext{s}}}{I_{{ ext{el}}}}}}{{2F}} $ | (A5) |
|
|
表 A1 光伏阵列仿真参数 Table A1 Simulation parameters of photovoltaic array |
|
|
表 A2 PEM电解槽阵列仿真参数 Table A2 Simulation parameters of PEM electrolyzer array |
|
|
表 A3 分段线性化中各子块拟合效果 Table A3 Fitting effect of sub blocks in piecewise linearization |


