动态优化笔记(一)
相对于求解函数极值这类静态问题,许多存在于真实世界的优化问题都是在动态变化的,这一类问题被称为动态优化问题,或动态环境优化问题。在这类问题中,目标函数、约束条件、帕累托前沿等都有可能随着时间进行变化。这一类动态优化问题比静态问题更有难度,随着时间推移,我们必须对一个问题进行重复优化。
动态优化问题的定义如下:
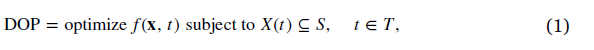
S是搜索空间
f是目标函数在时间t的取值
X(t)是在时间t的一组可行解
动态优化问题也可根据解向量的取值情况分为离散的和连续的,如下:

我们应该能够在任何时间,追踪到问题的最优值(近似值)。这需要我们在每次环境发生变化后,算法能快速收敛到全局最优,并且不被之前优化解所困而陷入局部最优。对于算法的性能测量,可以用离线性能(在K个时间段内的最优值相加的均值;offline performance)等,也可以从“算法在每次变化后得到的最优值与实际最优相距多少”,离线误差(offline error),准确度(Accuracy)等。
一般来说,算法的性能指标,可以分为基于最优值的和基于行为的,以上就是基于最优值的测量。而基于行为的测量,可以从解得多样性、稳定性、鲁棒性、交叉熵(不懂)、峰的覆盖、λ-branching(不懂)等几个方面取值。另外的性能指标,可以从评估算法跟踪和定位可行解的能力来进行评价。
当然,这些大部分是对于单目标来说的,对于多目标还有更多的性能测量方式。
1.The moving peaks 移动峰问题—MPB
2.The generalized dynamic benchmark generator —GDB
上一篇: 保障房和商品房是什么意思?区别有哪些?


